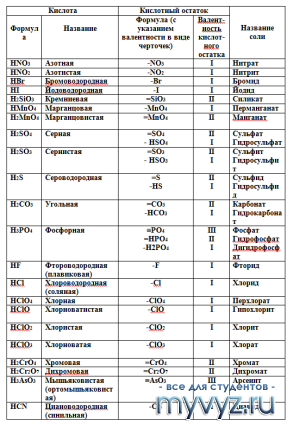
Шпора: Метод полуреакций, названия кислот и солей, некоторые вещества.
В данном архиве в .doc формате размещены:
- Метод полуреакций
- Названия кислот и солей компакт
- Названия кислот и солей
- Некоторые вещества
В 2009-ом году в зимнюю сессию мне здорово помог данный материал для успешной сдачи химии с третьего раза.
Рабочая тетрадь "Концепции современного естествознания"
ВВЕДЕНИЕ
1. ЭВОЛЮЦИЯ ЕСТЕСТВЕННОНАУЧНОЙ КАРТИНЫ МИРА
2. ПРОСТРАНСТВО, ВРЕМЯ, СИММЕТРИЯ
3. КОНЦЕПЦИИ СОВРЕМЕННОГО ЕСТЕСТВОЗНАНИЯ 3 ОБЛАСТИ МИКРОМИРА
4. КОНЦЕПЦИИ СОВРЕМЕННОГО ЕСТЕСТВОЗНАНИЯ, ОПИСЫВАЮЩИЕ БИОЛОГИЧЕСКИЙ УРОВЕНЬ ОРГАНИЗАЦИИ МАТЕРИИ
5. КОНЦЕПЦИИ СОВРЕМЕННОГО ЕСТЕСТВОЗНАНИЯ В ОБЛАСТИ МАКРОМИРА
6. КОНЦЕПЦИИ СОВРЕМЕННОГО ЕСТЕСТВОЗНАНИЯ В ОБЛАСТИ МЕГАМИРА
7. СОВРЕМЕННЫЕ ПРЕДСТАВЛЕНИЯ ОБ ЭВОЛЮЦИИ ВСЕЛЕННОЙ, ЗЕМЛИ, ЖИЗНИ
СПИСОК ЛИТЕРАТУРЫ
Домашнее задание (В - 5)
ДОМАШНЕЕ ЗАДАНИЕ по дисциплине Теплофизика, Вариант № 5
Задачи: Глава 1 №: (1,5,7,16,17,18,21,28), Глава 2 №: (6,9,18,20)
Глава 1 – Теплопроводность.
1. Температуры на поверхностях шамотной стенки, толщин которой δ=200 мм, равны:
t1 =1000°С t2=200oC. Коэффициент теплопроводности шамота изменяется в зависимости с температуры по уравнению λ = 0,813 + 0,000582 *t
Показать, что плотность теплового потока q, Вт/м2 , в случае линейной зависимости коэффициента теплопроводности от t может быть вычислена по формуле для постоянного коэффициент теплопроводности, взятого при средней температуре стенки. Найти ошибку в определении температуры в точках х=57,5; 110 и 157,5 мм, если вычисления производятся по значению коэффициента теплопроводности, среднему для
заданного интервала температур, и построить график распределения температур в стенке.
5. Толщину слоя красного кирпича в стенке топочной камеры, рассмотренной в задаче 4, решено уменьшить в 2 раза, а между слоями поместить слой засыпки из диатомитовой крошки, коэффициент теплопроводности которой λ = 0,113+ 0,00023*t.
Какую нужно сделать толщину диатомитовой засыпки, чтобы при тех же температурах на внешних поверхностях стенки, что и в задаче 4, потери теплоты оставались неизменными?
7. Вычислить потери теплоты через единицу поверхности кирпичной обмуровки парового котла в зоне размещения водяного экономайзера и температуры на поверхностях стенки, если толщина стенки δ, мм, температура газов tж1, ° С и воздуха в
котельной tж2, °С. Коэффициент теплоотдачи от газов к поверхности стенки α1, Вт/(м2 * К) и от стенки к воздуху α2, Вт/(м2 * К). Коэффициент теплопроводности λ, Вт/(м * К).
16. Резиновая пластина толщиной 2δ, мм нагретая до температуры tп, ° С помещена в воздушную среду с температурой tж, ° С. Определить температуры в середине и на поверхности пластины через τ = 20 мин после начала охлаждения. Коэффициент теплоотдачи от поверхности пластины к окружающему воздуху α, Вт/(М2 * К).
17. Для условий предыдущей задачи определить температуру на расстоянии х=δ/2, мм от середины пластины. Определить также безразмерные температуры в середине и на поверхности пластины расчетным путем и сравнить результаты расчета со значениями Θx=0 и Θx=δ полученными в задаче 16.
18. Определить промежуток времени по истечении которого лист стали, прогретый до температуры tп, ° С, будучи помещен в воздушную среду, температура которой tж, ° С, примет температуру, отличающую не более чем на 1% от температуры окружающей среды. Толщина листа 2δ, мм Коэффициент теплоотдачи от поверхности листа к окружающему воздуху α, Вт/(м2 * К). Указание: Для оценки характера распределения температуры по сечению листа необходимо воспользоваться формулой Θ= exp(-Bi*Fo), если Bi << 0,l
21. Определить значения температур на поверхности и на оси вала в условиях предыдущей задачи по истечении 25 и 40 мин после загрузки вала в печь.
28. В экспериментальной установке для определения коэффициент теплопроводности твердых тел методом регулярного режима исследуемый материал помещен в шаровой калориметр радиусом r = 30 мм. После предварительного нагрева калориметр охлаждается в воздушном термостате, температура в котором tж, ° С, поддерживается постоянной и равной 20 0 С. В результат, предварительных исследований установлено, что коэффициент теплоотдачи от поверхности калориметра к окружающему воздуху
α=7 Вт/(м2 * К) и коэффициент температуропроводности материал; α=3,37*10*-7 м/с.
Вычислить коэффициент теплопроводности исследуемого материала, если в процессе охлаждения после наступления регулярного режима температура в центре калориметра за ∆τ уменьшилась от t1 =27° С до t2 = 27o C
Глава 2 – Теплообмен излучением.
6. Нагрев стальной болванки осуществляется в муфельной электрической печи с температурой ее стенок tс, ° С. Степень черноты поверхности стальной болванки ε1 (средняя за период нагрева) и степень черноты шамотной стенки муфельной печи ε2. Площадь поверхности печи, участвующей в лучистом теплообмене F2.
9. Температура воздуха в помещении измеряется ртутным термометром. Термометр показывает t, ° С. Температура стен помещения равна tс, ° С.
Оценить ошибку в показаниях термометра, которая возникает за счет лучистого теплообмена между термометром и стенами помещения, и действительную температуру воздуха, приняв степень черноты стекла равной ε, а коэффициент теплоотдачи от воздуха к поверхности термометра α, Вт/(м2 * К).
18. В электрической муфельной печи высотой H, м шириной B, м нагревается плоская металлическая заготовка, расположенная на поду печи, до температуры tк м, ° С. Начальная температура заготовки равна tк H, ° С, ее степень черноты равна и не зависит от температуры; температура внутренней поверхности печи и ее степень черноты равны соответственно tc, 0 С, и ε. Определить плотность результирующего теплового потока на поверхности металла в начале, конце и ходе нагрева, когда его температура
составляет t, 0 С. При расчете принять, что заготовка покрывает практически весь под печи.
20. Температура продуктов сгорания, содержащих m % СO2 и n % Н2O равна t, ° С. Определить степень черноты продуктов сгорания и плотность потока собственного излучения их, если камерная печь имеет размеры: высота Н, м; ширина В, м; длина L, м.
Давление продуктов сгорания принять равным атмосферному.
1. Температуры на поверхностях шамотной стенки, толщин которой δ=200 мм, равны:
t1 =1000°С t2=200oC. Коэффициент теплопроводности шамота изменяется в зависимости с температуры по уравнению λ = 0,813 + 0,000582 *t
Показать, что плотность теплового потока q, Вт/м2 , в случае линейной зависимости коэффициента теплопроводности от t может быть вычислена по формуле для постоянного коэффициент теплопроводности, взятого при средней температуре стенки. Найти ошибку в определении температуры в точках х=57,5; 110 и 157,5 мм, если вычисления производятся по значению коэффициента теплопроводности, среднему для
заданного интервала температур, и построить график распределения температур в стенке.
5. Толщину слоя красного кирпича в стенке топочной камеры, рассмотренной в задаче 4, решено уменьшить в 2 раза, а между слоями поместить слой засыпки из диатомитовой крошки, коэффициент теплопроводности которой λ = 0,113+ 0,00023*t.
Какую нужно сделать толщину диатомитовой засыпки, чтобы при тех же температурах на внешних поверхностях стенки, что и в задаче 4, потери теплоты оставались неизменными?
7. Вычислить потери теплоты через единицу поверхности кирпичной обмуровки парового котла в зоне размещения водяного экономайзера и температуры на поверхностях стенки, если толщина стенки δ, мм, температура газов tж1, ° С и воздуха в
котельной tж2, °С. Коэффициент теплоотдачи от газов к поверхности стенки α1, Вт/(м2 * К) и от стенки к воздуху α2, Вт/(м2 * К). Коэффициент теплопроводности λ, Вт/(м * К).
16. Резиновая пластина толщиной 2δ, мм нагретая до температуры tп, ° С помещена в воздушную среду с температурой tж, ° С. Определить температуры в середине и на поверхности пластины через τ = 20 мин после начала охлаждения. Коэффициент теплоотдачи от поверхности пластины к окружающему воздуху α, Вт/(М2 * К).
17. Для условий предыдущей задачи определить температуру на расстоянии х=δ/2, мм от середины пластины. Определить также безразмерные температуры в середине и на поверхности пластины расчетным путем и сравнить результаты расчета со значениями Θx=0 и Θx=δ полученными в задаче 16.
18. Определить промежуток времени по истечении которого лист стали, прогретый до температуры tп, ° С, будучи помещен в воздушную среду, температура которой tж, ° С, примет температуру, отличающую не более чем на 1% от температуры окружающей среды. Толщина листа 2δ, мм Коэффициент теплоотдачи от поверхности листа к окружающему воздуху α, Вт/(м2 * К). Указание: Для оценки характера распределения температуры по сечению листа необходимо воспользоваться формулой Θ= exp(-Bi*Fo), если Bi << 0,l
21. Определить значения температур на поверхности и на оси вала в условиях предыдущей задачи по истечении 25 и 40 мин после загрузки вала в печь.
28. В экспериментальной установке для определения коэффициент теплопроводности твердых тел методом регулярного режима исследуемый материал помещен в шаровой калориметр радиусом r = 30 мм. После предварительного нагрева калориметр охлаждается в воздушном термостате, температура в котором tж, ° С, поддерживается постоянной и равной 20 0 С. В результат, предварительных исследований установлено, что коэффициент теплоотдачи от поверхности калориметра к окружающему воздуху
α=7 Вт/(м2 * К) и коэффициент температуропроводности материал; α=3,37*10*-7 м/с.
Вычислить коэффициент теплопроводности исследуемого материала, если в процессе охлаждения после наступления регулярного режима температура в центре калориметра за ∆τ уменьшилась от t1 =27° С до t2 = 27o C
Глава 2 – Теплообмен излучением.
6. Нагрев стальной болванки осуществляется в муфельной электрической печи с температурой ее стенок tс, ° С. Степень черноты поверхности стальной болванки ε1 (средняя за период нагрева) и степень черноты шамотной стенки муфельной печи ε2. Площадь поверхности печи, участвующей в лучистом теплообмене F2.
9. Температура воздуха в помещении измеряется ртутным термометром. Термометр показывает t, ° С. Температура стен помещения равна tс, ° С.
Оценить ошибку в показаниях термометра, которая возникает за счет лучистого теплообмена между термометром и стенами помещения, и действительную температуру воздуха, приняв степень черноты стекла равной ε, а коэффициент теплоотдачи от воздуха к поверхности термометра α, Вт/(м2 * К).
18. В электрической муфельной печи высотой H, м шириной B, м нагревается плоская металлическая заготовка, расположенная на поду печи, до температуры tк м, ° С. Начальная температура заготовки равна tк H, ° С, ее степень черноты равна и не зависит от температуры; температура внутренней поверхности печи и ее степень черноты равны соответственно tc, 0 С, и ε. Определить плотность результирующего теплового потока на поверхности металла в начале, конце и ходе нагрева, когда его температура
составляет t, 0 С. При расчете принять, что заготовка покрывает практически весь под печи.
20. Температура продуктов сгорания, содержащих m % СO2 и n % Н2O равна t, ° С. Определить степень черноты продуктов сгорания и плотность потока собственного излучения их, если камерная печь имеет размеры: высота Н, м; ширина В, м; длина L, м.
Давление продуктов сгорания принять равным атмосферному.
Расчет гидропривода. Курсовой проект.
По исходным данным спроектировать гидравлический привод с гидродвигателем поступательного движения, а также выбрать все необходимые гидроаппараты для нормального функционирования гидропривода.
Объектом исследования является объемный гидродвигатель, служащий для преобразования энергии рабочей среды в энергию движения выходного звена.
Цель работы — освоение навыков проектирования гидравлического привода поступательного движения.
Был произведен выбор: насосной установки, предохранительного клапана, дросселя, трубопровода, фильтрующего устройства.
Был произведен расчет: стенки гидроцилиндра, донной части гидроцилиндра, штока на устойчивость, теплового режима.
Учебное пособие по экспериментам
Раздел 1 Группировка и представление экспериментальных результатов.
Раздел 2. Статистическое оценивание экспериментальных результатов.
Раздел 2. Статистическое оценивание экспериментальных результатов.
Конспект лекций по дисциплине ОРГАНИЗАЦИЯ ЭКСПЕРИМЕНТА
Раздел 1. Понятие об эксперименте, группировка и представление эксперимен-тальных результатов
1.1. Понятие об эксперименте, опыте, качество эксперимента. Особенности эксперимен-тальных исследований металлургических процессов.
1.1.2. Особенности экспериментальных исследований металлургических процессов
1.1.2.1 Основные понятия теории вероятности и математической статистики
Статистики и точечная оценка
Законы распределения случайных величин
1. Гауссовское (нормальное) распределение
Нормированное нормальное распределение
2. Эмпирические распределения
1.2. Группировка и представление экспериментальных результатов. Вариационные ряды
Графическое изображение вариационных рядов
Раздел 2. Статистическое оценивание экспериментальных результатов
2.1. Понятие доверительного интервала и его вычисление для математического ожидания и дисперсии
2.1.1 Понятие доверительного интервала
2.1. Понятие доверительного интервала и его вычисление для математического ожидания и дисперсии
2.1.1 Понятие доверительного интервала
2.1.2. Построение доверительного интервала для математического ожидания при неизвест-ном
2.1.3. Построение доверительного интервала для дисперсии
2.2. Статистические гипотезы. Оценка значимости и точности экспериментальных результатов. Сравнение результатов измерений
Понятие о статистической гипотезе
2.2.2. Оценка значимости экспериментальных результатов
2.2.3. Проверка гипотезы о равенстве дисперсий (проверка точности)
2.2.4. Сравнение результатов измерений
2.3. Проверка гипотез о законе распределения экспериментальных результатов. Воспроизводимость экспериментальных результатов. Проверка адекватности
2.3.1. Проверка гипотез о законе распределения экспериментальных результатов
2.3.2. Проверка воспроизводимости результатов опытов
2.3.3. Проверка адекватности
Раздел 3. Основы дисперсионного анализа
3.1. Модель дисперсионного анализа, условия его проведения. Матрицы экспериментальных наблюдений
3.2. Анализ влияния одного или нескольких факторов на значения показателей качества. Алгоритм проведения анализа
Раздел 4. Корреляционный и регрессионный анализы
4.1. Функциональные и статистические связи между переменными. Модель корреляционно-го анализа
Основные положения корреляционного анализа
Коэффициент линейной корреляции
Свойства коэффициента линейной корреляции
Расчет коэффициента корреляции
4.2. Многомерный корреляционный анализ
Частная корреляция
Множественная корреляция
Использование корреляционного анализа
Ранжирование признаков и факторов
4.3. Модель и основные положения регрессионного анализа. Описание экспериментальных результатов функциональными зависимостями (моделями). Использование корреляционно-го и регрессионного анализа в практической деятельности.
4.3.1. Регрессионный анализ
4.3.2. Метод наименьших квадратов
4.3.3. Описания экспериментальных результатов функциональными зависимостями (моделями)
4.3.4. Оценка значимости коэффициентов регрессии (модели)
4.3.5. Построение доверительных интервалов для коэффициентов модели
4.3.6. Проверка значимости уравнения регрессии (адекватности)
Раздел 5. Основы математического планирования эксперимента. Факторные планы
5.1. Задачи математического планирования многофакторных экспериментов. Полный и дробный эксперимент для двухуровневых факторов
Реальные и кодированные значения уровней факторов
Полный факторный эксперимент (ПФЭ)
Регрессионная модель ПФЭ
Реализация плана ПФЭ
Рандомизация
Расчет коэффициентов уравнения регрессии
Дробный факторный эксперимент (ДФЭ) при K ≤ 2
Оценка воспроизводимости опытов
Оценка значимости коэффициентов уравнения
Упрощенная оценка значимости коэффициентов уравнения
Оценка адекватности модели
Факторное пространство
Поверхность отклика (функции)
Анализ математических моделей процессов
Раздел 6. Композиционные планы второго порядка. Метод главных эффектов
6.1. Принцип построения композиционного плана. Композиционная стратегия проведения опы-тов. Построение математических моделей второго порядка при использовании композиционных планов. Представление модели главных эффектов при различных уровнях факторов
6.2. Преобразование типовых планов в планы главных эффектов. Алгоритм построения математической модели процесса с использованием метода главных эффектов
Раздел 7. Планирование экспериментов для достижения оптимального значения показателей качества
7.1. Постановка задачи оптимизации при планировании экспериментов
Градиентные методы поиска экстремума
Метод крутого восхождения (Бокса-Уилсона)
Метод Гаусса-Зайделя
7.3. Симплексный метод нахождения значений факторов, обеспечивающих достижение заданного уровня показателей качества
1.1. Понятие об эксперименте, опыте, качество эксперимента. Особенности эксперимен-тальных исследований металлургических процессов.
1.1.2. Особенности экспериментальных исследований металлургических процессов
1.1.2.1 Основные понятия теории вероятности и математической статистики
Статистики и точечная оценка
Законы распределения случайных величин
1. Гауссовское (нормальное) распределение
Нормированное нормальное распределение
2. Эмпирические распределения
1.2. Группировка и представление экспериментальных результатов. Вариационные ряды
Графическое изображение вариационных рядов
Раздел 2. Статистическое оценивание экспериментальных результатов
2.1. Понятие доверительного интервала и его вычисление для математического ожидания и дисперсии
2.1.1 Понятие доверительного интервала
2.1. Понятие доверительного интервала и его вычисление для математического ожидания и дисперсии
2.1.1 Понятие доверительного интервала
2.1.2. Построение доверительного интервала для математического ожидания при неизвест-ном
2.1.3. Построение доверительного интервала для дисперсии
2.2. Статистические гипотезы. Оценка значимости и точности экспериментальных результатов. Сравнение результатов измерений
Понятие о статистической гипотезе
2.2.2. Оценка значимости экспериментальных результатов
2.2.3. Проверка гипотезы о равенстве дисперсий (проверка точности)
2.2.4. Сравнение результатов измерений
2.3. Проверка гипотез о законе распределения экспериментальных результатов. Воспроизводимость экспериментальных результатов. Проверка адекватности
2.3.1. Проверка гипотез о законе распределения экспериментальных результатов
2.3.2. Проверка воспроизводимости результатов опытов
2.3.3. Проверка адекватности
Раздел 3. Основы дисперсионного анализа
3.1. Модель дисперсионного анализа, условия его проведения. Матрицы экспериментальных наблюдений
3.2. Анализ влияния одного или нескольких факторов на значения показателей качества. Алгоритм проведения анализа
Раздел 4. Корреляционный и регрессионный анализы
4.1. Функциональные и статистические связи между переменными. Модель корреляционно-го анализа
Основные положения корреляционного анализа
Коэффициент линейной корреляции
Свойства коэффициента линейной корреляции
Расчет коэффициента корреляции
4.2. Многомерный корреляционный анализ
Частная корреляция
Множественная корреляция
Использование корреляционного анализа
Ранжирование признаков и факторов
4.3. Модель и основные положения регрессионного анализа. Описание экспериментальных результатов функциональными зависимостями (моделями). Использование корреляционно-го и регрессионного анализа в практической деятельности.
4.3.1. Регрессионный анализ
4.3.2. Метод наименьших квадратов
4.3.3. Описания экспериментальных результатов функциональными зависимостями (моделями)
4.3.4. Оценка значимости коэффициентов регрессии (модели)
4.3.5. Построение доверительных интервалов для коэффициентов модели
4.3.6. Проверка значимости уравнения регрессии (адекватности)
Раздел 5. Основы математического планирования эксперимента. Факторные планы
5.1. Задачи математического планирования многофакторных экспериментов. Полный и дробный эксперимент для двухуровневых факторов
Реальные и кодированные значения уровней факторов
Полный факторный эксперимент (ПФЭ)
Регрессионная модель ПФЭ
Реализация плана ПФЭ
Рандомизация
Расчет коэффициентов уравнения регрессии
Дробный факторный эксперимент (ДФЭ) при K ≤ 2
Оценка воспроизводимости опытов
Оценка значимости коэффициентов уравнения
Упрощенная оценка значимости коэффициентов уравнения
Оценка адекватности модели
Факторное пространство
Поверхность отклика (функции)
Анализ математических моделей процессов
Раздел 6. Композиционные планы второго порядка. Метод главных эффектов
6.1. Принцип построения композиционного плана. Композиционная стратегия проведения опы-тов. Построение математических моделей второго порядка при использовании композиционных планов. Представление модели главных эффектов при различных уровнях факторов
6.2. Преобразование типовых планов в планы главных эффектов. Алгоритм построения математической модели процесса с использованием метода главных эффектов
Раздел 7. Планирование экспериментов для достижения оптимального значения показателей качества
7.1. Постановка задачи оптимизации при планировании экспериментов
Градиентные методы поиска экстремума
Метод крутого восхождения (Бокса-Уилсона)
Метод Гаусса-Зайделя
7.3. Симплексный метод нахождения значений факторов, обеспечивающих достижение заданного уровня показателей качества
ДЗ по экспериментам
Построение гистограммы.
Оценка значимости.
Расчет доверительного интервала для дисперсии.
Проверка гипотезы о равенстве центров распределения.
Проверка гипотезы о равенстве дисперсий.
Проверка гипотезы о законе распределения.
Оценка значимости.
Расчет доверительного интервала для дисперсии.
Проверка гипотезы о равенстве центров распределения.
Проверка гипотезы о равенстве дисперсий.
Проверка гипотезы о законе распределения.
ГИДРАВЛИКА Учебное пособие
М.Я. Кордон, В.И. Симакин, И.Д. Горешник
ГИДРАВЛИКА Учебное пособие
Учебное пособие подготовлено на основе опыта многолетнего
преподавания курса «Гидравлика».
При изложении материала учтены такие предпосылки, как
логическая связь с другими дисциплинами специальности 330200;
фундаментальность представления теоретических вопросов; прак-
тическая направленность рассматриваемых вопросов;
использование математического аппарата в объеме, не
превышающем доступности восприятия теоретического материала.
Учебный материал подготовлен в соответствии с рабочей про-
граммой и охватывает следующие разделы: основные физические
свойства жидкостей; основы гидростатики; основы кинематики и
динамики жидкости; гидравлический удар в трубах; основы теории
подобия, моделирования и анализа размерностей; основы
движения грунтовых вод и двухфазных потоков.
В каждом разделе рассмотрены примеры практического
применения расчетных формул и зависимостей в виде примеров
задач и различных инженерных решений.
Представлен также перечень контрольных вопросов для само-
стоятельного изучения материала.
Курс «Гидравлика» является одной из основополагающих
дисциплин при подготовке инженеров, работающих в области
защиты окружающей природной среды.
Теоретический материал сопровождается иллюстрациями в
виде рисунков, графиков, блок-схем и таблиц в объеме, требующем
пояснения качественной или количественной связи параметров
технологических процессов или физических явлений.
Авторы учебного пособия учли ценные замечания рецензентов
и выражают им свою признательность.